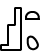3. Termin 2: Das "Go-Back-N"-Protokoll

Zur Vorbereitung arbeiten Sie bitte die Folien der Vorlesung für das „Go-Back-N“-Protokoll der Unit 10 (ARQ Approach) und dieses Kapitel durch.

Der Großteil der in diesem Kapitel aufgelisteten Anpassungen wurden bereits für Sie umgesetzt. Das gesamte System finden Sie in Ihrem Home-Bereich im Verzeichnis BlockC/ T2_GBNProtokoll und die wichtigsten Teile des Systems (Transmitter, TransmitterQueue und Receiver) im Skript. Der Transmitter kommuniziert mit dem Prozess TransmitterQueue, in dem die gesendeten Rahmen gespeichert werden bis sie quittiert werden (die RetransmissionQueue). Dieser Prozess braucht nicht beachtet werden und kann als gegeben vorausgesetzt werden. Außerdem braucht das Medium nicht näher untersucht werden, das eine Queue verwendet, in der Rahmen gespeichert werden, bis sie an den Receiver ausgeliefert werden. Damit das zur Verfügung gestellte System entsprechend der Spezifikationen des Protokolls funktioniert, müssen noch an 3 Stellen Fehler im SDL-Quellcode korrigiert werden.

Bei den bisher betrachteten Protokollen — „Send-and-Wait“ und „Alternating-Bit“ — befindet sich jeweils nur ein Paket im Medium: Nachdem der Sender ein Datenpaket versendet hat, wartet dieser auf eine Quittung vom Empfänger. Diese Vorgehensweise ist äußerst ineffizient, da der Kanal die meiste Zeit nicht belegt ist. Anstelle zu pausieren und nur auf die Quittung zu warten, könnten bereits weitere Pakete vom Sender übertragen werden.

Deshalb betrachten wir im folgenden Abschnitt das „Go-Back-N“- Protokoll. Grundsätzlich werden beim „Go-Back-N“- Protokoll Pakete gesendet ohne auf Quittungen (engl. Acknowledgement) der Pakete vom Empfänger zu warten. Diese kontinuierliche Übertragung von Paketen hat eine Erhöhung des Durchsatzes zur Folge, insbesondere dann, wenn eine geringe Bitfehlerwahrscheinlichkeit im Medium zu beobachten ist.

Dieses Kapitel wird zunächst einen Überblick über die allgemeine Funktionsweise des Protokolls geben. Anschließend wird eine analytische Leistungsanalyse zur Berechnung des Durchsatzes durchgeführt. Dadurch sind wir in der Lage, zu überprüfen, ob die Ergebnisse der anschließenden Experimente sinnvolle Ergebnisse zur Folge haben. Bei den Experimenten soll die Abhängigkeit des Durchsatzes von der Bitfehlerwahrscheinlichkeit im Medium und seine Abhängigkeit von der Fenstergröße näher analysiert werden.

4.1 Funktionsweise des „Go-Back-N"-Protokolls

Zu diesem Zweck enthält jeder Rahmen eine fortlaufende Sequenznummer. Erst, wenn die Anzahl der gesendeten Rahmen identisch mit der maximalen Fenstergröße ist, muss auf den Empfang einer Quittung gewartet werden. Eine Quittung vom Empfänger enthält eine Information darüber, wie viele Rahmen der Empfänger korrekt empfangen hat. Dieser Mechanismus hat zur Folge, dass der Durchsatz gegenüber dem „Alternating-Bit“-Protokoll ansteigt und gleichzeitig der Empfänger durch die eingebaute Flusskontrolle nicht überlastet wird.

In diesem Abschnitt gehen wir auf das grundlegende Verhalten des Protokolls ein und nutzen die Beispiele aus Abb. 8 und Abb. 9.

Für die Funktionsweise des „Go-Back-N“-Protokolls wird zwischen zwei Fällen unterschieden:

fehlerfreie Übertragung: In diesem Fall werden alle Datenpakete und deren Quittungen fehlerfrei übertragen.
fehlerbehaftete Übertragung: Hierbei ist die Bitfehlerrate p>0. Es werden fehlerhafte Pakete und deren Folgepakete erneut übertragen.

4.1.1 Der fehlerfreie Fall

Bei fehlerfreier Übertragung sendet der Sender kontinuierlich mit fortlaufenden Sequenznummern versehene Datenpakete über das Medium an den Empfänger. Der Empfänger quittiert korrekt empfangene Pakete mit der Sequenznummer des letzten erfolgreich und in korrekter Reihenfolge erhaltenen Paketes.

Beispiel:

Beim MSC in Abb. 8 stellt der gezeigte Fall die fehlerfreie Übertragung dar. Man erkennt, dass alle vom Sender verschickten Pakete im Abstand von $t_I+t_p$ den Empfänger erreichen. Nach einer Verarbeitungszeit $t_{proc}$ quittiert der Empfänger jedes korrekt empfangene Datenpaket mit einem Acknowledgment (kurz ACK), das nach der Zeit $t_s+t_p$ vom Sender empfangen wird. Hierbei gilt, dass die Sequenznummer eines ACKs immer das letzte in korrekter Reihenfolge empfangene Paket des Senders beinhaltet. Nach dem ersten empfangenen Paket ist dies "0", dann "1, "2", usw.

Anmerkung:

$t_I$ - beschreibt das Transmission-Delay eines Datenpaketes und ist definiert als die Bitrate dividiert durch die Paketgröße.
$t_s$ - beschreibt das Transmission-Delay einer Quittung und ist definiert als die Bitrate dividiert durch die Größe des Quittungs- Paketes.
$t_p$ - beschreibt das Propagation-Delay.

Abb. 8: Message Sequence Chart (MSC) für den fehlerfreien Fall, für das GBN-Protokoll ohne Flusskontrolle

4.1.2 Der fehlerbehaftete Fall

Wie beim „Alternating-Bit“- oder „Send-and-Wait“-Protokoll, startet der Sender des „Go-Back-N“-Protokolls auch einen Retransmission-Timer für jedes versendete Paket. Läuft der Timer vor Erhalt der Quittung ab (z. B. durch Verlust eines Pakets im Medium), werden alle Pakete ab jenem, für das der Timer abgelaufen ist, erneut übertragen.

Ähnlich verhält es sich, wenn eine Quittung verloren gegangen ist: Der Sender erhält nicht die erwartete Quittung - vor Ablauf des Retransmissiontimers - und überträgt alle bis zu dem Zeitpunkt unbestätigten Pakete erneut.

Anmerkung:

In der Regel werden kumulative Quittungen verwendet. Dies bedeutet, eine Quittung alle zuvor gesendeten Pakete auch quittiert. Hierdurch wird der Einfluss von verloren gegangenen ACK reduziert. Demnach interpretiert das Protokoll nicht am Sender erhaltene ACKs als empfangen, sobald das Acknowlegment eines späteren Pakets den Sender erreicht.

Beispiel:

Beim MSC in Abb. 9. stellt der erste, farblich rot markierte Abschnitt den Fall der fehlerhaften Übertragung dar. Man erkennt, dass das Paket mit der Sequenznummer „m“ punktiert dargestellt ist und nicht den Empfänger erreicht, da es im Medium verloren gegangen ist. Alle folgenden vom Sender verschickten Pakete (mit den Sequenznummern „m+1“, „m+2“, usw.) erreichen den Empfänger fehlerfrei. Da das Paket mit der Sequenznummer „m+1“ nicht jener am Empfänger erwarteten „m“ entspricht, werden alle im Folgenden empfangene Pakete verworfen und mit der Quittung des letzten korrekten Paketes „m-1“ bestätigt. Erst nachdem der Retransmissiontimer für Paket „m“ nach tout abgelaufen ist, wird die erneute Übertragung aller unbestätigten Pakete gestartet. Dies ist der als Fehlerbehebung bezeichnete und orange markierte Abschnitt in Abb. 9..

Abb. 9: Message Sequence Chart (MSC) für den fehlerhaften (rot) Fall mit anschl. Fehlerbehebung (orange) für das GBN-Protokoll ohne Flusskontrolle

4.2 Leistungsfähigkeit des „Go-Back-N“-Protokolls ohne Flusskontrolle

Literaturhinweis: Dieses Kapitel ist stark am Buch „Telecommunication Networks — Protocols, Modeling and Analysis“, Addison-Wesley, 1988 von Mischa Schwartz angelehnt. I.d.R. stammen die Formeln und Abbildungen aus diesem Werk.

Gesucht wird die Dauer, die im Mittel benötigt wird, um ein Paket erfolgreich zum Empfänger zu übertragen. Erfolgreich übertragen bedeutet hierbei, dass das Paket den Empfänger fehlerfrei und in korrekter/erwarteter Reihenfolge erreicht.

Wie bei der Beschreibung der Funktionsweise des "Go-Back-N"- Protokolls (siehe Kapitel 4.1), wird bei der Herleitung der Dauer der mittleren Übertragungszeit eines Pakets zwischen der fehlerfreien und der fehlerbehafteten Übertragung unterschieden.

Zur Vereinfachung der Herleitung, werden die im Folgenden getroffenen Annahmen verwendet. Diese Vereinfachungen können dazu führen, dass die Ergebnisse der Herleitung zu abweichenden Ergebnissen gegenüber realen Experimenten führen:

Die möglichen Sequenznummern einzelner Pakete seien nicht beschränkt.
Keine negative Quittungen: Ein Paket wird erst erneut gesendet, wenn der Retransmission-Timer abgelaufen ist. Wurde zuvor eine Quittung empfangen, die vermuten lässt, das ein Paket nicht empfangen wurde, dann wird diese Quittung ignoriert.
Die Verarbeitungsgeschwindigkeit des Empfängers $t_{proc}$ ist zu vernachlässigen. Genauer: Sie ist sehr viel größer als die Übertragungsgeschwindigkeit des Kanals und die Verarbeitungsgeschwindigkeit des Senders. Dies bedeutet, dass keine Flusskontrolle (engl. Congestion Control) notwendig ist.
Es liege in diesem Modell eine gesättigte Übertragung vor. Dies bedeutet, dass permanent Daten zur Übertragung seitens des Senders zur Verfügung stehen.
Es seien alle Paketlängen und der Wert des Retransmission-Timers $t_{out} = 2t_I + 2t_p $ konstant.
Die Dauer zur Übertragung einer Quittung ts sei kleiner als die eines Pakets.

Abb. 10: GBN-Analyse für fehlerfreie Übertragung (oben) und fehlerbehaftete Übertragung (unten)

Der Wert $t_T = t_I + t_{out}$ beschreibt die Dauer, die pro fehlerhaftem Übertragungsversuch vergeht, ehe die erneute Übertragung beginnt.

Mittlere Übertragungszeit eines Pakets im fehlerfreien Fall

Durch die kontinuierliche Übertragung benötigt jedes Paket die Dauer von $t_I$ zur Übertragung. Da beim "Go-Back-N"-Protokoll nicht auf ein Acknowledgment gewartet wird, ehe das Folgepaket übertragen werden kann, beträgt die mittlere Übertragungszeit $t_V$ eines Paketes im fehlerfreien Fall:

$$ t_V = t_I \tag{1} $$

Der maximal erreichbare Durchsatz (Pakete/Sekunde) berechnet sich nun aus dem reziproken Wert der mittleren Übertragungszeit. Es gilt folglich:

$$ D_{max} = \frac{1}{t_V} = \frac{1} {t_I} \tag{2} $$

Mittlere Übertragungszeit eines Pakets im fehlerbehafteten Fall

Die Bitfehlerwahrscheinlichkeit betrage nun p. Somit ist die Wahrscheinlichkeit dafür, dass ein Bit fehlerfrei übertragen wird gegeben als

$$ 1-p \tag{3} $$

In diesem statistischen System mit der Bitfehlerwahrscheinlichkeit p, wird nun das folgendes Ereignis näher betrachtet:
Die erste Übertragung eines Paketes ist mit der Wahrscheinlichkeit p fehlerbehaftet und/aber der zweite Versuch der Übertragung eines Pakets ist mit der Wahrscheinlichkeit (1-p) erfolgreich. Für dieses spezielle Ereignis wird die mittlere Übertragungszeit $t_V$ gesucht.
Dieses spezielle Ereignis hat die Wahrscheinlichkeit $p \cdot (1-p)$ und tritt immer dann ein, wenn der Sender für die Dauer des Retransmission- Timeout-Intervalls $t_{out}$ auf das entsprechende Acknowledgment wartet. Danach kann der erste Übertragungsversuch der fehlerhaften Übertragung mit der Dauer $t_T= t_{out}$ als abgeschlossen betrachtet werden.

Nachfolgend ist dann die Übertragung erfolgreich und hat die Dauer $t_I$. Demnach ist die mittlere Übertragungszeit:

$$ t_V = \overbrace{t_I}^{erfolgreiche \ Übertragung} + \overbrace{\underbrace{(1-p)}_{Wahrscheinlichkeit \\ fehlerfreier \ Übertragung.} \cdot \underbrace{1p \cdot t_T}_{Wahrscheinlichkeit \ fehlerhafter \\ Übertragung \ inkl. \ Dauer}}^{Dauer \ einer \ fehlerhaften \ Übertragung} \tag{4} $$

Ist auch dieser erneute Übertragungsversuch fehlgeschlagen, dann erreicht ein Paket erst nach dem dritten Übertragungsversuch den Empfänger (bzw. das ACK den Sender), so erhöht sich $t_V$ um den 3. Summationsterm in Gleichung (5) ehe das Paket erfolgreich den Empfänger erreicht.

$$ t_V = \overbrace{t_I}^{erfolgr. \ Übertr.} + \underbrace{(1-p) \cdot 1p \cdot t_T}_{Dauer \ der \ ersten \\ fehlerhaften \ Übertr.} + \underbrace{(1-p) \cdot 2p^2 \cdot t_T}_{Dauer \ der \ zweiten \\ fehlerhaften \ Übertr.} \tag{5} $$

Man erkennt hieraus bereits die folgende, allgemeine Bildungsvorschrift:

$$ t_V = \overbrace{t_I}^{(i+1)-te \ Übertragung \\ (erfolgreich)} + \overbrace{(1-p) \cdot \sum_{i=1}^{\infty} ip^i \cdot t_T}^{i \ Übertagungen \\ (fehlerhaft)} \tag{6} $$

Die mittlere Übertragungszeit für ein erfolgreich am Empfänger angekommenes Paket $tV$ erhöht sich abhängig davon, wie oft es erneut übertragen werden muss

Wiederholung mathematischer Grundlagen: Wie eventuell noch aus den mathematischen Grundlagen-Modulen bekannt ist, handelt es sich hierbei um eine geometrische Reihe. Aufgrund dieser Tatsache, kann die Summe vereinfacht und dadurch ersetzt werden. Für geometrische Reihen gilt allgemein:

$$ (1-q) \cdot \sum_{k=0}^{\infty}q^k = 1 - q^{n+1} \tag{7} $$

Für q ungleich 1 lässt sich die Gleichung durch (1-q) teilen:

$$ \sum_{k=0}^{\infty} {q^k} = \frac{q^{n+1} -1 } {q-1} = \frac{1-q^{n+1}} {1-q} \\ \lim_{n \rightarrow \infty} \frac{1-q^{n+1}} {1-q} = \frac{1} {1-q} \tag{8} $$

Vorfaktoren — wie in unserem Fall tT — können problemlos aus der Summe gezogen werden.

Dennoch enthält unsere Folge zusätzlich die Gauß'sche Summenformel. Somit folgt für die mittlere Übertragungsdauer eines Paketes:

$$ \begin{align} t_V &= t_{I} + (1-p) \cdot t_T \cdot \sum_{i=1}^{\infty}{ip^i} \\ &= t_{I} \cdot \left( \frac{1-p+\frac{t_T}{t_I}\cdot p}{1-p} \right) \\ &= t_I \cdot \left( \frac{1+(a-1) \cdot p}{1-p} \right), \ \ \ mit \ a = \frac{t_T}{t_I} \\ \end{align} \tag{9} $$

wobei p die Bitfehlerwahrscheinlichkeit und a=tT/tI beschreibt. Falls die Ausbreitungszeit tp und Verarbeitungszeit ts verglichen mit der Übertragungsdauer tI vernachlässigbar sind und somit a=1 gilt, entsprechen die Ergebnisse jenen vom SnW-Protokoll. Der reziproke Wert beschreibt den maximal möglichen Durchsatz. Es gilt:

$$ D_{max} = t_V^{-1} = \frac{1-p}{1+(a-1) \cdot p \cdot t_I} \tag{10} $$

wobei der normalisierte Durchsatz r für jede Paketankunftsrate D ist:

$$ \rho = D \cdot t_I < \frac{1-p}{1+(a-1) \cdot p} \tag{11} $$

Beispiel: Gegeben sei eine terrestrische Verbindung mit einer Kapazität von 9600 Bits/s und einer festen Paketlänge von 1200 Bits. Sei der Link kürzer als 160 km und sei das propagation delay etwa 1 ms/160 km, so ist das round-trip propagation delay maximal 2 ms.

Bestimmen Sie die Übertragungsdauer und dem idealen Wert für den Retransmission-Timer.

Lösung: $t_I$ = 1200 b/9600 bps = 125 ms, $t_{out} = 2 t_p + t_{proc} + t_s$

Wie bereits zuvor beschrieben, sollte der Wert für $t_{out}$ nicht zu klein gewählt werden. Es benötigt somit mindestens $ 2t_p+t_s$, bis eine Bestätigung den Sender erreicht. Werden die Bestätigungen in separaten Paketen gesendet, benötigt dieses zusätzlich $t_I$. Um sicherzugehen, wird der Wert für $t_{out}$ daher auf $2t_p+2t_I$ gesetzt.

Somit folgt für die minimale Zeit zwischen zwei erfolgreich übertragenen Paketen: $t_T=t_I+t_{out}=3t_I+2t_p$. Für $a=\frac{t_T}{t_I}$ folgt $3+\frac{2tp}{tI}$. Dieses kontinuierliche GBN-Protokoll führt somit zu einer Durchsatzerhöhung gegenüber dem einfachen Send-and-Wait Protokoll von a > 3.

In der folgenden Abbildung sind drei Verläufe des Durchsatzes über der Paketlänge dargestellt. Jede Kurve stellt dabei eine bestimmte Art der Übertragung dar (Sat, WLAN und LAN), die sich bezüglich ihrer Fehlerrate und Propagation-Delay unterscheiden.

Abb. 11: Durchsatz-Verläufe am Beispiel 3 charakt. Technologien

4.2.1 Go-Back-N mit Flusskontrolle

Beim in Kapitel 4.2 betrachteten Go-Back-N Protokoll wird das Medium in der Regel komplett ausgelastet. Hierdurch kann es vorkommen, dass der Empfänger oder das Netzwerk zeitweilig überlastet wird. Die unbeschränkte senderseitige Übertragung von Datenpaketen wird nun mithilfe der Flusskontrolle reguliert. Hierzu definiert das Go-Back-N Protokoll die Fenstergröße M, die die Anzahl der maximal vom Sender zu übertragenen Pakete an den Empfänger begrenzt. Beim Erreichen dieser Grenze, pausiert der Sender mit der Übertragung weiterer Pakete und wartet auf eine Quittung seitens des Empfängers.

Der fehlerfreie Fall

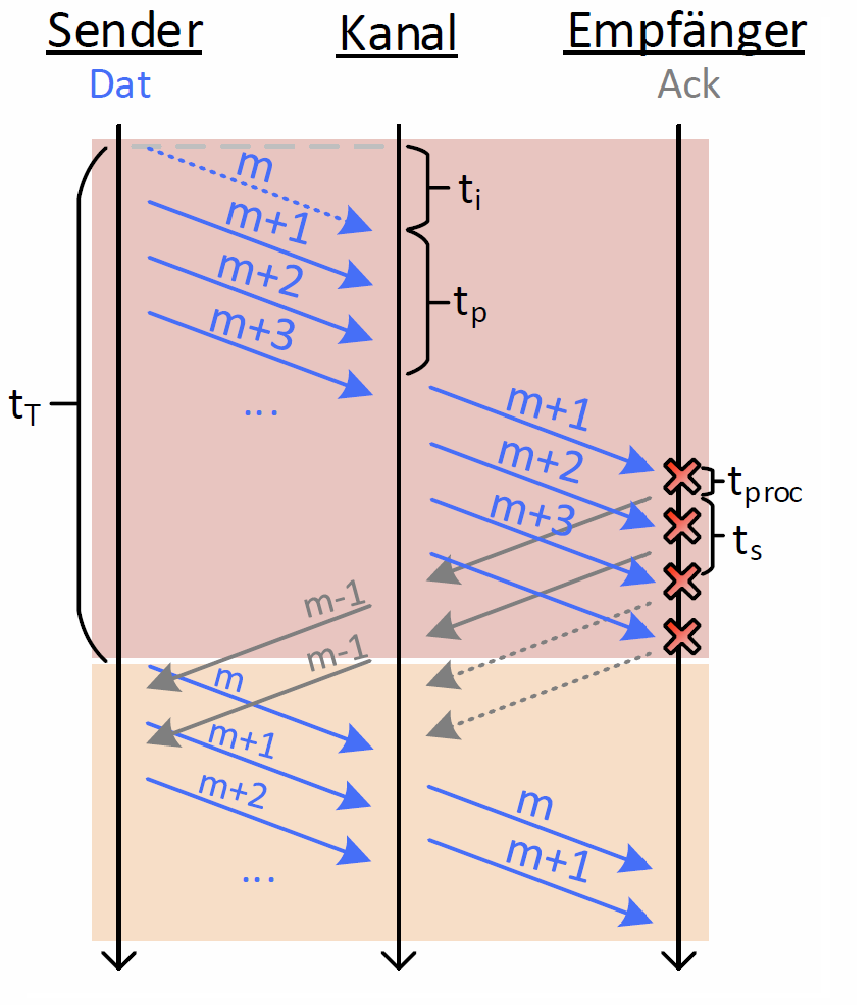
Im fehlerfreien Fall sendet der Sender M Datenpakete an den Empfänger, wobei M die Fenstergröße beschreibt. In Abb. 34, ist M=3, sodass der Sender erst auf eine Quittung seitens des Empfängers warten muss, ehe er weitere Pakete (n+3, n+4, ...) versenden darf.

Nach der Dauer $t_{ack}$ erreicht den Sender die Quittung zum korrespondierenden Paket - in diesem Beispiel ist dies die Quittung für das Paket mit der Sequenznummer „n“ - sodass folglich das Folgepaket versendet werden darf. $t_{ack}$ ist hierbei die Summe aus den Propagation-Verzögerungen für das Datenpaket und Acknowlegment (also $2t_p$) und der Verzögerung zur Übertragung eines ACK ($t_s$). Es gilt: $t_{ack}=2t_p+t_s$. Da die Acknowlegments für die Pakete eines Fensters nahezu hintereinander den Sender erreichen, kann dieser nun auch wieder Folgepakete übertragen entsprechend der Fenstergröße.

Abb. 12: GBN-Protokoll mit Flusskontrolle für fehlerfreie Übertragung und der Fenstergröße 3

Die erfolgreiche Übertragung eines einzelnen Paketes beträgt $t_I + t_p$. Somit beträgt die Übertragungsdauer für M Pakete abhängig der Fenstergröße insgesamt $M \cdot t_I + t_p$

Im Vergleich zum Kapitel 4.2 limitiert nun die Fenstergröße M die maximale Anzahl zu sendender und unbestätigter Pakete.

Nachdem der Sender die maximal mögliche Anzahl an Paketen versendet hat, muss dieser mit der Übertragung pausieren und zwar solange, bis er eine Bestätigung seitens des Empfängers erhält. Die Dauer bis die Bestätigung den Sender erreicht beträgt $t_s + t_p$. Der Einfachheit halber wird für ein ACK die identische Übertragungsdauer eines Datenpaketes verwendet (Quittungen haben aufgrund ihrer geringeren Paketgröße eine viel kürzere Übertragungsdauer), sodass $t_s=t_I$ gilt.

In der Abb. 12 werden $2t_p$ (1x für die Datenpakete und 1x für die Bestätigung) und $t_s=t_I$ zu $t_{ack}$ zusammengefasst. Somit erhält man für die mittlere Übertragungsdauer $t_V$ pro Paket abhängig der Fenstergröße:

$$ t_V = \frac{M \cdot t_I + t_{ack}}{M} \ \ \ \ , \ mit \ t_{ack} = 2 \cdot t_p +t_I \tag{12} $$

Der Durchsatz berechnet sich aus dem reziproken Wert der mittleren Übertragungsdauer und es gilt:

$$ D = t_V^{-1} = \frac{M}{M \cdot t_I + t_{ack}} \ \ \ \ , \ mit \ t_{ack} = 2 \cdot t_p +t_I \tag{13} $$

Zur Überprüfung des Ergebnisses der Gl. (13) betrachten wir nun die Grenzfälle für eine extrem kurze Propagation-Verzögerung und jener, die ein Vielfaches höher als die Transmission-Verzögerung ist:

$$ \lim_{t_p \rightarrow 0} D = \frac{1} {t_I} \tag{14} $$

und

$$ \lim_{t_p \gg t_I} D = M \cdot \frac{1} {t_p} \tag{15} $$

Es zeigt sich:

Ist das Propagation-Delay vernachlässigbar (siehe Gl. (14)), erhält man das selbe Ergebnis wie für das Go-Back-N Protokoll ohne Flusskontrolle (siehe Kapitel 4.2). Bei hohem Propagation-Delay nimmt der Durchsatz linear mit steigender Fenstergröße zu (siehe Gl. (14)).

Der fehlerbehaftete Fall.

Die Bitfehlerwahrscheinlichkeit betrage nun erneut p>0. Analog zum fehlerbehafteten Fall ohne Flusskontrolle, verhält sich das System auch mit Flusskontrolle: Erreicht ein Datenpaket nicht den Empfänger, so wird der Sender keine Quittung für dieses Paket innerhalb des Timeout-Intervalls erhalten. Sobald der Retransmission-Timer abgelaufen ist, überträgt der Sender das gesamte Fenster erneut und wartet anschließend auf die Quittungen.

Daher ähnelt die Berechnung des Durchsatzes mit Flusskontrolle stark der Berechung des Durchsatzes ohne Flusskontrolle (siehe Gl. (6)).

Wir werden daher erneut den Durchsatz mit Hilfe der mittleren Übertragungsdauer eines Paketes, $t_V$, bestimmen. Zusätzlich zur Dauer, die für die erfolgreiche Übertragung benötigt wird, erhöht sich $t_V$ bei jedem fehlerhaften Übertragungsversuch:

Es wird vergeblich auf das entsprechende ACK gewartet, ehe die erneute Übertragung des Fensters beginnt. Analog zum Durchsatz ohne Flusskontrolle, können die fehlerhaften Übertragungsversuche durch eine geometrische Reihe beschrieben werden.

$$ t_V = \overbrace{\frac{M \cdot t_I + t_{ack}}{M}}^{erfolgreiche \ Übertragung} + \overbrace{ \sum_{n=1}^{\infty} n \cdot \underbrace{(1-p) \cdot p^n}_{Wahrscheinlichkeit} \cdot \underbrace{t_T(M)}_{Dauer}}^{n \ fehlerhafte \ Übertragungen} \tag{16} $$

Wie man deutlich in Gl. (16) erkennen kann, ist die Dauer einer fehlerhaften Übertragung, $t_T$, nun abhängig von der Fenstergröße M.

Aus diesem Grund wird zwischen zwei Fällen unterschieden. Die Dauer der fehlerhaften Übertragung tT variiert, je nachdem, ob der Retransmission-Timer bereits während der Übertragung des Fensters abläuft oder erst, nachdem das Fenster komplett versendet wurde.

Diese beiden Fälle werden wir nun genauer betrachten:

Als erstes sei die Dauer des Retransmissiontimers $t_{out}$ kürzer als die benötigte Zeit, um alle Pakete innerhalb eines Fensters zu übertragen. Die Dauer, um das gesamte Fenster zu übertragen, beträgt: $M \cdot t_I$.

Abb. 13 visualisiert dies, wobei in diesem Beispiel die Fenstergröße M=5 betrage: Das rot-markierte Paket mit der Sequenznummer „n“ erreiche den Empfänger nicht oder fehlerhaft und wird dem Sender nicht quittiert. Man erkennt, dass dem fehlerbehafteten Paket eines Fensters noch (M-1) Pakete folgen.

Abb. 13: GBN mit Flusskontrolle für fehlerbehaftete Übertragung mit Fenstergröße 5 (Fall 1)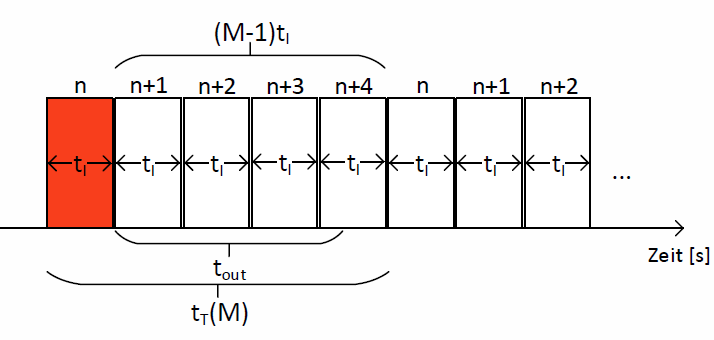

Da der Retransmissiontimer $t_{out}$ innerhalb der Übertragung innerhalb eines Fensters abläuft gilt:

Nachdem der Retransmissiontimer $t_{out}$ abgelaufen ist, muss der Sender warten bis der Sendepuffer leer ist, d.h. alle zuvor gesendeten Pakete übertragen wurden. Hierzu wird die Zeit $(M-1) \cdot t_I$ benötigt. Nun erst kann das fehlerhafte Paket mit der Dauer $t_I$ und alle Folgepakete erneut übertragen werden. Demnach ist:

$$ t_T(M) = (M -1) \cdot t_I + t_I $$
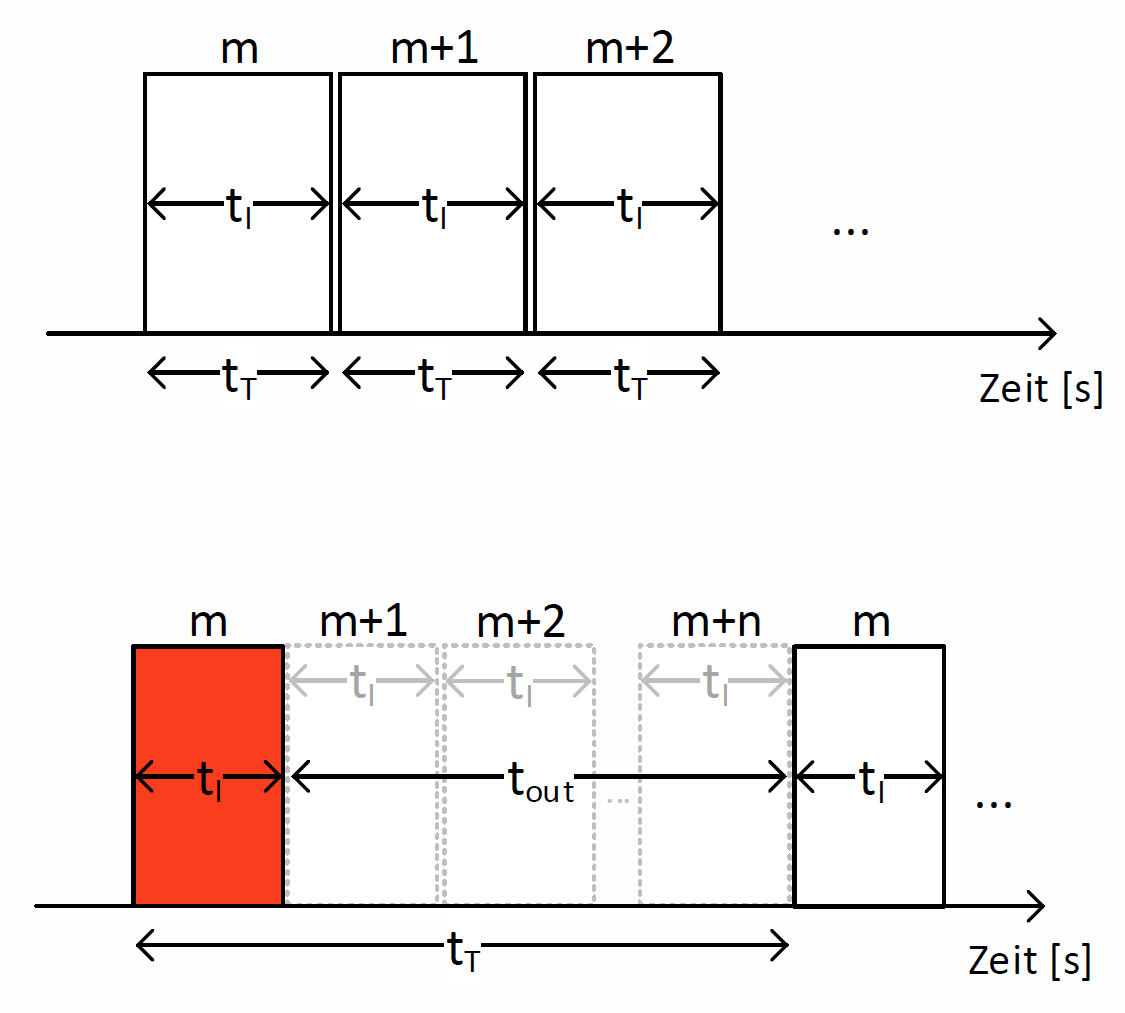
Widmen wir uns nun dem Fall bei dem tout größer ist als die Zeit, die benötigt wird, um das gesamte Fenster der Größe M zu übertragen. Zur Visualisierung verwenden wir dafür Abb. 36. Auch für diesen Fall betrage die Fenstergröße M=5 und das rot-markierte Paket „n“ erreicht den Empfänger nicht bzw. fehlerhaft und wird nicht quittiert.

Da die Dauer des Retransmissiontimers $t_{out}$ nun größer ist als die Dauer, die der Sender zur Übertragung des gesamten Fensters M benötigt, ist der Kanal für eine gewisse Zeit frei. Dies ist durch den grau-schraffierten Bereich kenntlich gemacht. Erst nachdem der Retransmissiontimer $t_{out}$ abgelaufen ist, wird die erneute Übertragung des gesamten Fensters gestartet.

Abb. 14: GBN mit Flusskontrolle für fehlerbehaftete Übertragung mit Fenstergröße 5 (Fall 2)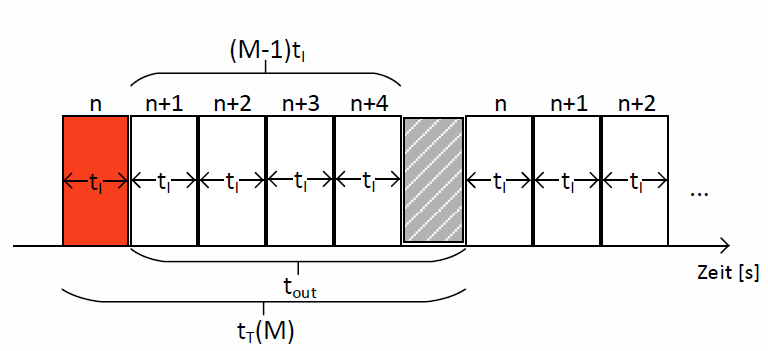

Zusätzlich zur Dauer, die vergeblich auf das Acknowledgment gewartet wird, muss erneut die Übertragungsdauer des fehlerhaften Paketes berücksichtigt werden. Es gilt:

$$ t_T = t_{out} + t_I $$

Nachdem wir nun die beiden möglichen Fälle für die Dauer, nachdem die erneute Übertragung eines Fensters beginnt, betrachtet haben, wissen wir, dass dieser Wert $t_T$ grundsätzlich nicht nach oben beschränkt, wohl aber nach unten durch die Fenstergröße begrenzt ist. Um die oben genannte Formel für beide Fälle anwenden zu können, definieren wir $t_T(M)$ zu dem höheren der beiden möglichen Werte. Es gilt:

$$ t_T(M) = max\{t_{out},(M-1) \cdot t_I\} \tag{17}$$

Setzt man dies in die Gleichung von tV ein, so erhält man für die mittlere Übertragungsdauer pro Paket:

$$ t_V = \frac{M \cdot t_I + t_{ack}}{M} + \sum_{n=1}^{\infty} (1-p) \cdot p^n \cdot n \cdot (max\{t_{out},(M-1)t_I\}+t_I) \tag{18} $$

Für den Durchsatz gilt erneut der reziproke Wert der mittleren Übertragungsdauer:

$$ D_{max} = t_V^{-1} \tag{19} $$

Der relative Durchsatz berücksichtigt die Nutzdatengröße eines Rahmens und die vorhandene Bitrate des Links:

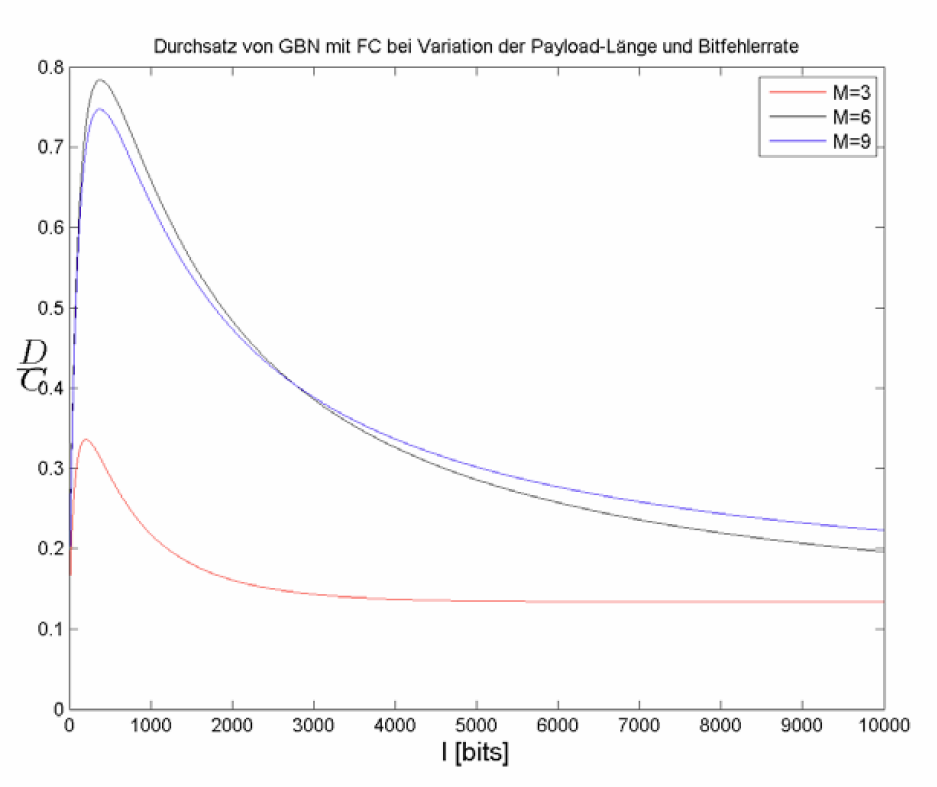
$$ \frac{D}{C} = \frac{D_{max} \cdot l }{C} = \frac{l}{t_V C} \tag{20} $$

Abb. 15: Durchsatzverläufe mit Flusskontrolle bei Variation der Fenstergröße

Wie bereits Abb. 11 im Fall ohne Flusskontrolle, visualisiert Abb. 15 die erreichbaren Durchsatzraten.

4.3 Umsetzung des „Go-Back-N“-Protokolls

Entsprechend der kurzen Beschreibung des „Go-Back-N“-Protokolls ist ersichtlich, welche Modifikationen beim „Alternating-Bit“-Protokoll durchgeführt werden müssen damit daraus ein Go-Back-N Protokoll wird:

Es muss eine Konstante MaxWindow eingeführt werden, die den Wert der maximalen Fenstergröße (engl. window size) angibt.
Es muss eine Variable eingeführt und initialisiert werden, die den Wert der augenblicklichen Fenstergröße symbolisiert. Window gibt an, wie viele unquittierte Pakete noch versendet werden dürfen.
Es muss die Variable NS im Transmitter eingeführt werden, die die Nummer des nächsten zu sendenden Rahmens angibt. Die Variable NR des Transmitters gibt die Nummer des letzten in korrekter Reihenfolge empfangenen Rahmens an. Die Differenz zwischen NS und NR ist die Anzahl der Rahmen, die sich auf dem Weg zwischen Sender und Empfänger befinden.
Es muss die Variable VS eingeführt werden. Eine Quittung des Empfangers enthält die Rahmennummer VS, die der nächste Rahmen des Senders haben muss bzw. von ihm erwartet wird.
Das folgende Beispiel im fehlerfreien Fall soll diese Verhalten veranschaulichen:
- Als ersten Rahmen der Rahmen mit der Sequenznummer "0" gesendet.
- Die Variable NR hat den Wert "0".
- Der Empfänger wird nach Empfang des Rahmens "0" eine Quittung mit der Sequenznummer "1" senden.
- Daraufhin wird der Sender die Variable NR aud den Wert "1" setzen und den Rahmen mit der Squenznummer "1" senden.
- ... usw.

Alle das Protokoll betreffenden grundlegenden Eigenschaften sollten aus der Vorlesung bekannt sein, sodass Sie wissen, wie sich das Protokoll mit über das Medium erzeugten Fehlern verhält.

Verständnisfragen:

Die Fenstergröße beträgt 5. Sie senden die Pakete mit den Sequenznummern 0..4. Was passiert, wenn das Paket mit der Sequenznummer 3 verloren geht

Was wird erneut gesendet? Nach welchem Ereignis geschieht das? Hat die Fenstergröße Einfluss auf die Wahl der Sequenznummern? . . . )

Ein weiteres Beispiel: Das Acknowledgement für das erste Paket geht verloren. Was passiert?

4.4 Laboraufgaben

Korrigieren Sie die Fehler im SDL-Diagramm und testen Sie die Funktionsweise des „Go-Back-N“-Protokolls im reliable Mode und Loose-Mode. Setzen Sie hierzu die Fenstergröße auf den Wert 4. Im Loose-Mode soll jedes 3. Paket verloren gehen. Speichern Sie die MSCs und werten diese im Protokoll zum Block C aus. Für diesen Versuch werwenden Sie bitte das Skript Trial1: Test GoBackN-Protocol. Passen Sie das Skript an ihre Bedürfnisse an.

Zeigen Sie durch Simulationen im reliable Mode, wie sich die maximale Fenstergröße auf den erzielten Durchsatz zwischen den Prozessen Source und Destination auswirkt. Verwenden Sie hierfür das Skript Trial2: Throughput vs. Windowsize. Hierzu notieren Sie sich den Wert der Variablen now und berechnen den erzielte Durchsatz. Variieren Sie die Fenstergröße vom Wert 1 bis zum Wert 32 durch Ändern der Variable Window im Sript.

Bestimmen Sie den Durchsatz des „Go-Back-N“-Protokolls unter dem Einfluss von Bitfehleren. Verwenden Sie dabei den Bitfehlergenrerator der Bitfehler entsprechend einer Exponentialverteilung erzeugt, indem sie die Varaible MsgErrorDistr auf "1" einstellen. Es wird empfohlen für diesen Versuch das bereitgestellte Skript Trial3: Throughput vs. MeanBitErrorRate zu nutzen. Die Bedeutung der Parameter können leicht nachvollzogen werden.
Hierfür noch einige Hinweise:
- Es ist nicht notwenig die Simulation zu verfolgen während sie läuft. Setzen sie also die Trace-Level auf "0" und verzichten sie auf einen interaktiven MSC-Log. Auf diese Weise ist das Ergebnis eines Messpunktes praktisch ohne Verzögerung
  Bei sehr hohen Fehlerraten (also kleinen MsgErrMean Werten) und hoher Paket Anzahl kann es dennoch zu Simulationszeiten von einigen Sekunden bis Minuten kommen. Sie benötigen jedoch nicht sehr viele Messpunkte an dieser Stelle.
  erhältlich. Anderenfalls können die Messungen mehrere Stunden dauern!
- Sie erhalten von SDT als Ergebnis lediglich die Variable "now". Überlegen Sie sich, wie Sie aus der Variable "now" den Durchsatz berechnen können. Welche Parameter werden noch benötigt?
- Mit der Variable MsgErrMean stellen sie den Kehrwert der mittleren Fehlerwarscheinlichkeit ein. Sinnvolle Werte sind im Bereich von [1 100000] zu finden. Wird MsgErrMean" z.B. auf "2" gesetzt, dann ist im mittel jedes 2. Bit fehlerhaft. Bedenken sie, dass sie vorallem mehrere Messpunkte für mittlere bis geringe Fehlerraten (p<0.3) benötigen! Eine logarithmische Verteilung kann sinnvoll sein!
- Senden sie nicht weniger als 10000 Pakete (für den voreingestellte Breakpoint für DataConf also mindestens 20000!) pro Messpunkt! Dadurch erhalten sie zuverlässigere Ergebnisse.